Differential RCS

Differential RCS characterizes the aptitude of a tag to modulate the backscattered power. This parameter is has been introduced by P. Nikitin for UHF tags and is classically estimated based on the variation of the IQ channels of the two states of the chip in the time domain. This quantity can however be generalized for any modulating tag in the frequency domain. The frequency definition remains (almost) compatible to the time definition. Finally, this new definition allows to estimate the delta RCS of any tag accurately using a simple spectrum analyzer.

Definition

Fig. 1: Power spectral density of the signal backscattered by a modulating tag in the frequency domain.

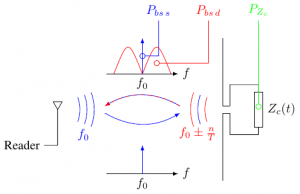
Details have been presented in and can be seen as a complementary definition compared to the time definition. The basic idea relies on the decomposition of the RCS $\sigma$ into a static RCS Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_s} and a dynamic RCS $\sigma _{d}$ and to pass into the frequency domain. Fig. 1 presents the main result where the (total) backscattered signal by the modulating UHF tag can be decomposed into 2 parts. Component located at $f_{0}$ can be linked to $\sigma _{s}$ whereas component located around $f_{0}$ can be linked to $\sigma _{d}$.

Also, this frequency definition (as the original definition) is not limited to RFID tags and can be applied to any linear time-varying system such as rotating tags, moving tag and (surprisingly) barcodes. Another consequence is that linear time-invariant systems, are characterized by a delta RCS of 0.

Known Differential RCS

• For a UHF tag, assuming that the chip can switch with a equal probability in-between 2 states characterized with $\Gamma _{1}$ and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Gamma_2} , and is connected to a half-wavelength antenna, the delta RCS Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_d} can be expressed as:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_d = \frac{\lambda^2 G^2}{4 \pi} \frac{|\Gamma_1 - \Gamma_2|^2}{4} }

At 915 MHz, this equation predicts a maximal delta RCS for passive (i.e., $\{\Gamma _{1}=0;\Gamma _{2}=-1\})$ and semi-passive (i.e., Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \{\Gamma_1 = +1; \Gamma_2=-1\})} UHF tags of -22 dBsm (63 cmFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle ^2} ) and -16 dBsm (250 cm$^{2}$) respectively.

• For a vertical dipole oriented along Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z} rotating at a frequency $f_{r}$ located at a distance $r$ of its axis and impinged by a vertical plane, the delta RCS of this rotating dipole can simply be expressed as:

$\sigma _{d}=(1-J_{0}(\beta ))\sigma$

where $J_{n}$ are the first kind Bessel function of order Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n} , $\beta ={\frac {2\pi r}{\lambda }}$ and $\sigma$ is the RCS of the dipole. Note that in this case variation of the backscattered power is continuous.

Measurement

Measurement method is based on the measurement of the modulated PSD of the backscattered signal $S_{R}(f-f_{0})$ which can be directly estimated by any spectrum analyzer. Delta RCS can finally be expressed as:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_d = \frac{(4\pi)^3 d_1^2 d_2^2}{P_t G_t G_r \lambda^2} \times \left[\int_{f_0-b}^{f_0-\epsilon} S_R(f-f_0)\,\mathrm{d}f + \int_{f_0+\epsilon}^{f_0+b} S_R(f-f_0)\,\mathrm{d}f\right] }

where $2b$ is the span of the instrument and $\epsilon$ a constant allowing to remove the static contribution generated by the tag (and the environment).