Differential RCS
Differential RCS (or delta RCS) characterizes the aptitude of a tag to modulate the backscattered power. This parameter is has been introduced by P. Nikitin for UHF tags [1] and is classically estimated based on the variation of the IQ channels of the two states of the chip in the time domain. This quantity can however be generalized for any modulating tag in the frequency domain. The frequency definition remains compatible to the time definition. Finally, this new definition allows to estimate the delta RCS of any tag accurately using a simple spectrum analyzer.
Definition
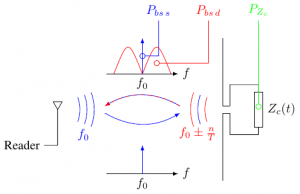
Details have been presented in [2] and can be seen as a complementary definition compared to the time definition. The basic idea relies on the decomposition of the RCS into a static RCS and a dynamic RCS and to pass into the frequency domain. Fig. 1 presents the main result where the (total) backscattered signal by the modulating UHF tag can be decomposed into 2 parts. Component located at can be linked to whereas component located around can be linked to .
Also, this frequency definition (as the original definition) is not limited to RFID tags and can be applied to any linear time-varying system such as rotating tags, moving tag and (surprisingly) barcodes. Another consequence is that linear time-invariant systems, are characterized by a delta RCS of 0.
Known Delta RCS
- For a UHF tag, assuming that the chip can switch with a equal probability in-between 2 states characterized with and , and is connected to a half-wavelength antenna, the delta RCS can be expressed as:
At 915 MHz, this equation predicts a maximal delta RCS for passive (i.e., and semi-passive (i.e., UHF tags of -22 dBsm (63 cm) and -16 dBsm (230 cm) respectively.
- For a multi-state transponder (i.e. a transponder which can switch its internal impedance between different values), its differential RCS can be expressed as [3]:
This quantity is generally sightly lower than the previous case but allows one to increase the data rate and/or the spectral efficiency.
- For a vertical dipole oriented along rotating at a frequency located at a distance of its axis and impinged by a vertical plane wave, the delta RCS of this rotating dipole can simply be expressed as:
where are the first kind Bessel function of order , and is the RCS of the dipole. Note that in this case variation of the backscattered power is continuous.
For a short-circuited half-wavelength dipole at 915 MHz, rotating at a distance of cm, delta RCS is equal to -10 dBsm (920 cm) which outperforms any UHF tag.
- For a scatterer characterized by a polarization scattering matrix equal to rotating in a plan which is normal to propagation vector and impinged by a vertical plane wave, the delta RCS of this rotating dipole can simply be expressed as [4]:
Note that the delta RCS is the same whatever the polarization of the reader antenna.
For a short-circuited half-wavelength dipole at 915 MHz, rotating in the previously described configuration, delta RCS is equal to -19.4 dBsm (115 cmFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle ^2} ).
Measurement
Measurement method is based on the measurement of the modulated PSD of the backscattered signal Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_R(f-f_0)} which can be directly estimated by any spectrum analyzer. Delta RCS can finally be expressed as:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_d = \frac{(4\pi)^3 d_1^2 d_2^2}{P_t G_t G_r \lambda^2} \times \left[\int_{f_0-b}^{f_0-\epsilon} S_R(f-f_0)\,\mathrm{d}f + \int_{f_0+\epsilon}^{f_0+b} S_R(f-f_0)\,\mathrm{d}f\right] }
where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2b} is the span of the instrument and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon} a constant allowing to remove the static contribution generated by the tag (and the environment).
References
- ↑ P. V. Nikitin, K. V. S. Rao, and R. D. Martinez, “Differential RCS of RFID tag,” Electronics Letters, vol. 43, no. 8, pp. 431–432, Apr. 2007.
- ↑ N. Barbot, O. Rance, and E. Perret, "Differential RCS of modulated tag," IEEE Transactions on Antennas and Propagation, pp. 1–1, 2021, early access. doi: 10.1109/TAP.2021.3060943.
- ↑ A. Voisin, A. Dumas, N. Barbot and S. Tedjini, “Differential RCS of Multi-State Transponder,” 2022 IEEE Wireless Power Week Conference (WPW 2022), Bordeaux, France, Jul. 2022, pp. 1–4.
- ↑ N. Barbot, "Delta RCS Expression of Linear Time-Variant Transponders based on Polarization Modulation," in 2022 IEEE RFID Technology and Applications Conference (RFID-TA), Cagliari, Italy, Sep. 2022, pp. 1–4.











![{\displaystyle \sigma _{d}={\frac {\lambda ^{2}G^{2}}{4\pi }}\left[\sum _{i}p_{i}|\Gamma _{i}-\Gamma _{s}|^{2}\right].}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/ffdb397ea1dc251a751ad57bf251d8b3e2d4872d)



![{\displaystyle \sigma _{d}=[1-J_{0}(\beta )]\sigma }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/6597afbdc02ec9bf91a92a6145db5a4ed8fa7f3b)





