Differential RCS

Differential RCS (or delta RCS) characterizes the aptitude of a tag to modulate the backscattered power. This parameter is has been introduced by P. Nikitin for UHF tags and is classically estimated based on the variation of the IQ channels of the two states of the chip in the time domain. This quantity can however be generalized for any modulating tag in the frequency domain. The frequency definition remains compatible to the time definition. Finally, this new definition allows to estimate the delta RCS of any tag accurately using a simple spectrum analyzer.

Definition

Fig. 1: Power spectral density of the signal backscattered by a modulating tag in the frequency domain.

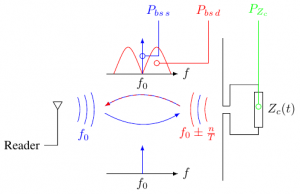
Details have been presented in and can be seen as a complementary definition compared to the time definition. The basic idea relies on the decomposition of the RCS Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma} into a static RCS $\sigma _{s}$ and a dynamic RCS $\sigma _{d}$ and to pass into the frequency domain. Fig. 1 presents the main result where the (total) backscattered signal by the modulating UHF tag can be decomposed into 2 parts. Component located at $f_{0}$ can be linked to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_s} whereas component located around $f_{0}$ can be linked to $\sigma _{d}$.

Also, this frequency definition (as the original definition) is not limited to RFID tags and can be applied to any linear time-varying system such as rotating tags, moving tag and (surprisingly) barcodes. Another consequence is that linear time-invariant systems, are characterized by a delta RCS of 0.

Known Delta RCS

• For a UHF tag, assuming that the chip can switch with a equal probability in-between 2 states characterized with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Gamma_1} and $\Gamma _{2}$, and is connected to a half-wavelength antenna, the delta RCS $\sigma _{d}$ can be expressed as:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_d = \frac{\lambda^2 G^2}{4 \pi} \frac{|\Gamma_1 - \Gamma_2|^2}{4} }

At 915 MHz, this equation predicts a maximal delta RCS for passive (i.e., Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \{\Gamma_1 = 0; \Gamma_2=-1\})} and semi-passive (i.e., $\{\Gamma _{1}=+1;\Gamma _{2}=-1\})$ UHF tags of -22 dBsm (63 cm$^{2}$) and -16 dBsm (230 cm$^{2}$) respectively.

• For a multi-state transponder (i.e. a transponder which can switch its internal impedance between $N$ different values), its differential RCS can be expressed as :

$\sigma _{d}={\frac {\lambda ^{2}G^{2}}{4\pi }}\left[\sum _{i}p_{i}|\Gamma _{i}-\Gamma _{s}|^{2}\right].$

• For a vertical dipole oriented along $z$ rotating at a frequency $f_{r}$ located at a distance $r$ of its axis and impinged by a vertical plane, the delta RCS of this rotating dipole can simply be expressed as:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma_d = [1 - J_0(\beta)] \sigma }

where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle J_n} are the first kind Bessel function of order $n$, $\beta ={\frac {2\pi r}{\lambda }}$ and $\sigma$ is the RCS of the dipole. Note that in this case variation of the backscattered power is continuous.

For a short-circuited half-wavelength dipole at 915 MHz, rotating at a distance of $r=12.5$ cm, delta RCS is equal to -10 dBsm (920 cmFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle ^2} ) which outperforms any UHF tag.

Measurement

Measurement method is based on the measurement of the modulated PSD of the backscattered signal $S_{R}(f-f_{0})$ which can be directly estimated by any spectrum analyzer. Delta RCS can finally be expressed as:

$\sigma _{d}={\frac {(4\pi )^{3}d_{1}^{2}d_{2}^{2}}{P_{t}G_{t}G_{r}\lambda ^{2}}}\times \left[\int _{f_{0}-b}^{f_{0}-\epsilon }S_{R}(f-f_{0})\,\mathrm {d} f+\int _{f_{0}+\epsilon }^{f_{0}+b}S_{R}(f-f_{0})\,\mathrm {d} f\right]$

where $2b$ is the span of the instrument and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon} a constant allowing to remove the static contribution generated by the tag (and the environment).