Differential RCS

Differential RCS characterizes the aptitude of a tag to modulate the backscattered power. This parameter is has been introduced by P. Nikitin for UHF tags and is classically estimated based on the variation of the IQ channels of the two states of the chip in the time domain. This quantity can however be generalized for any modulating tag in the frequency domain. The frequency definition remains (almost) compatible to the time definition. Finally, this new definition allows to estimate the delta RCS of any tag accurately using a simple spectrum analyzer.

Fig. 1: Power spectral density of the signal backscattered by a modulating tag in the frequency domain.

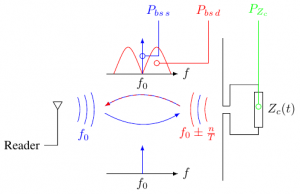
Details have been presented in and can be seen as a complementary definition compared to the time definition. The basic idea relies on the decomposition of the RCS $\sigma$ into a static RCS $\sigma _{s}$ and a dynamical RCS $\sigma _{d}$ and to pass into the frequency domain. Fig. 1 presents the main result where the (total) backscattered signal by the modulating UHF tag can be decomposed into 2 parts. Component located at $f_{0}$ can be linked to $\sigma _{s}$ whereas component located around $f_{0}$ can be linked to $\sigma _{d}$.

Measurement method is based on the measurement of the modulated PSD of the backscattered signal. This modulated power can be directly measured by any spectrum analyzer. Delta RCS can finally be expressed as: Failed to parse (unknown function "\begin{multline}"): {\displaystyle \begin{multline} \sigma_d = \frac{(4\pi)^3 d_1^2 d_2^2}{P_t G_t G_r \lambda^2}\\ \times \left[\int\displaylimits_{f_0-b}^{f_0-\epsilon} S_R(f-f_0)\,\mathrm{d}f + \int\displaylimits_{f_0+\epsilon}^{f_0+b} S_R(f-f_0)\,\mathrm{d}f\right] \label{final} \end{multline} }

Also, this frequency definition (as the original definition) is not limited to RFID tags and can be applied to any linear time-varying system such as rotating tags, moving tag and (surprisingly) barcodes. Another consequence is that linear time-invariant systems, are characterized by a delta RCS of 0.