Difference between revisions of "SC311 Wireless Communications"
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The objective of this course is to understand how we can transmit a message in-between a transmitter and a receiver spatially separated. Especially, how we can use signal processing operations to adapt (i.e. modulate and demodulate) the message to realize the transmission over wired or wireless channels. This course describes the processes realized at a signal level and can be related to [[MA331 Information Theory and Channel Coding]] (which presents the general problem at a higher level). | The objective of this course is to understand how we can transmit a message in-between a transmitter and a receiver spatially separated. Especially, how we can use signal processing operations to adapt (i.e. modulate and demodulate) the message to realize the transmission over wired or wireless channels. This course describes the processes realized at a signal level and can be related to [[MA331 Information Theory and Channel Coding]] (which presents the general problem at a higher level). | ||
Slides of the course can be downloaded here. Exercises can be downloaded here. The following of this page corresponds to the labs. | Slides of the course (in french) can be downloaded [https://nicolas-barbot.ovh/wiki/pool/CM.pdf here]. Exercises can be downloaded [https://nicolas-barbot.ovh/wiki/pool/TD.pdf here]. The following of this page corresponds to the labs. | ||
__TOC__ | __TOC__ | ||
| Line 93: | Line 93: | ||
<math> | <math> | ||
s(t) = A m(t) \cos 2 \pi f_0 t | |||
</math> | </math> | ||
* Observe the signal in both time and frequency domain. | * Observe the signal in both time and frequency domain. | ||
* Give the architecture of a coherent detector used to recover the message <math>m(t)</math> from <math> | * Give the architecture of a coherent detector used to recover the message <math>m(t)</math> from <math>s(t)</math>. | ||
* Implement this detector to demodulate the signal and verify the good operation. You can use 2 different flowgraphs (1 for the transmission and 1 for the reception) using a <syntaxhighlight lang="text" inline>File Sink</syntaxhighlight> and <syntaxhighlight lang="text" inline>File Source</syntaxhighlight> respectively. | * Implement this detector to demodulate the signal and verify the good operation. You can use 2 different flowgraphs (1 for the transmission and 1 for the reception) using a <syntaxhighlight lang="text" inline>File Sink</syntaxhighlight> and <syntaxhighlight lang="text" inline>File Source</syntaxhighlight> respectively. | ||
=== Double side band | === Double side band with carrier === | ||
* Realize the modulation of a signal <math>m(t)=\cos 2\pi f_m t</math> using a double side band with carrier. Note that transmitted signal can be expressed as | * Realize the modulation of a signal <math>m(t)=\cos 2\pi f_m t</math> using a double side band with carrier. Note that transmitted signal can be expressed as | ||
| Line 109: | Line 109: | ||
<math> | <math> | ||
s(t) = A (1 + k_a m(t)) \cos 2 \pi f_0 t | |||
</math> | </math> | ||
| Line 130: | Line 130: | ||
== Frequency Modulation == | == Frequency Modulation == | ||
= | Expression of a frequency modulated signal is given by: | ||
<math> | |||
s(t) = A \cos(2\pi f_0 t + 2\pi k_f \int_0^t m(u) du) | |||
</math> | |||
Spectrum for general signal is usually unknown unless for very simple cases. | |||
* Create the following flowgraph to generate a frequency (or phase) modulated signal. | |||
[[File:Fm1.png|frame|center|Fig. 4: Frequency modulation generation.]] | |||
* Observe the transmitted spectrum. | |||
* Find the values of the modulation index <math>\beta</math> to cancel the power at <math>f_0</math>, <math>f_0\pm f_m</math>, <math>f_0\pm 2f_m</math>... | |||
* Create a decoder for the transmitted signal. Check the correct operation for different messages <math>m(t)</math> | |||
Latest revision as of 14:25, 7 November 2023
The objective of this course is to understand how we can transmit a message in-between a transmitter and a receiver spatially separated. Especially, how we can use signal processing operations to adapt (i.e. modulate and demodulate) the message to realize the transmission over wired or wireless channels. This course describes the processes realized at a signal level and can be related to MA331 Information Theory and Channel Coding (which presents the general problem at a higher level).
Slides of the course (in french) can be downloaded here. Exercises can be downloaded here. The following of this page corresponds to the labs.
In this labs, we will realize different modulations and demodulations used to transmit and receive analog and digital messages. Spectrum (or power spectral density) will also be determined. Finally, performance, in term of Sinal to Noise Ratio (SNR) or Bit Error Rate (BER) will be estimated in each case.
These labs are based on GNU Radio which is a free software that provides a large number of software blocks to perform most signal processing operations. The blocks are mostly written in C ++. It is possible to use these blocks directly from Python to simulate or create telecommunication systems.
In addition, to make it easier to get started, GNU Radio also provides a utility called gnuradio-companion to assemble blocks graphically and to generate the corresponding python script. This subject have been written for GNU Radio, but it can be equivalently realized using Octave, or IT++ library.
Getting Started
- Open a terminal.
- Create a working directory in which you will place your scripts.
- Run
gnuradio-companion.
This software allows you to use blocks (available in the right column) and to connect them to realize any complex signal processing operations. Resulting program is called a flowgraph in GNU Radio language.
For any flowgraph, there is basically 3 types of blocks: sources (which produce samples and have at least 1 output), sinks (which consume samples and have at least 1 input) and processing block (which have at least 1 input and 1 output). Blocks are simply connected by creating a link in-between an output of a block and an input of another block.
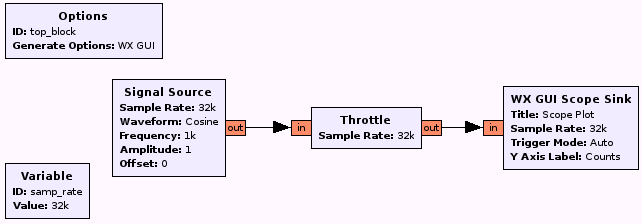
- Create the flowgraph presented in Fig. 1.
The Signal Source block generates an infinity of sinusoidal samples (or other) from the different parameters. These samples are displayed according to the time using the Scope Sink block. Throttle block does not modify the samples but allows to perform a flow control on all the data circulating between the source and the sink. Last, be careful to the color of the input and output of each block since they represent the type of data flowing on the link. The following table presents main data type and associated used by GNU Radio. Also, since Python is strongly typed, colors located at both ends of a wire have to be the same.
| Color | Type | Size |
|---|---|---|
| Complex | 2 x 64 bits | |
| Float | 64 bits | |
| Int | 64/32 bits | |
| Short | 16 bits | |
| Char | 8 bits |
- Save the flowgraph under your directory. This file is saved with a
.grcextension.
- Generate the associated Python script associated to your flowgraph using the "blue to red" button. If errors are present, the script is not generated and full listing is present under the no entry sign. When successful, observe the python script named
top_block.pyin your directory.
- Execute the script by pressing the run button. Equivalently, you can also invoke
python top_block.py.
The execution should display an oscilloscope-like widow with the corresponding signal (a cosine function). You can stop the execution by closing the window or by pressing the stop button.
- Check the amplitude and the period of the generated signal.
- Finally, add a
Sliderblock to modify the frequency of the signal in real time (without recompiling the flowgraph) and check the operation on the scope. Save the flowgraph.
Note that the source simply generates samples which are plotted by the sink, however, this source and this sink can produce and consume as much data that your CPU can handle (data are just generated and plotted iteratively as fast as possible). To overcome this issue, the Throttle block is used to process a given number of sample per second, thus lowering the CPU load to few percents. Most of the blocks in GNU Radio do not fixed the rate at which samples are processed: when sufficient number of samples are present at the input, the considered function is called and produces samples at the output which are then available for the other blocks. Usually, this rate is fixed when we work with real devices (for example an audio card can acquire samples at a given frequency e.g. 48 kHz) which fixed the rate for the whole flowgraph. In our example, we do not use any real device so the rate has to be fixed using the Throttle block. Also, for each flowgraph, a single rate has to be used thus if we work with a real device, the Throttle block is not needed anymore and has to be removed.
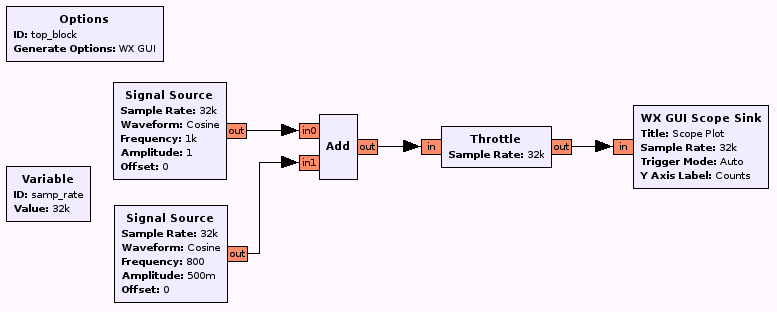
- Create the flowgraph presented in Fig. 2.
- Add a
FFT Sinkto observe the signal spectrum. On the graph, the two peaks are very close and seem to be confused. Reduce the frequency sampling to increase the frequency resolution. Explain the phenomenum.
- What is the minimum value of the sampling frequency? Observe the signal (in time and in frequency) for frequencies below this limit.
- Replace the
Addblock with a multiplier blockMult. Predict the position of the peaks in the output signal. Check your results.
- Add a filter (block
Low Pass Filter) to recover the low frequency part of the signal. Check your results in the time and frequency domain. Repeat the manipulation to keep the high frequency part.
The Low Pass Filter (and High Pass Filter) blocks are high-level blocks which realize the design (i.e. determining the coefficients of the filter) as well as the filtering (i.e. the convolution). The filter design can also be done with gr_filter_design to obtain the coefficients. These coefficients can then be used directly by the blocks FIR Filter and IIR Filter.
Amplitude Modulation
Double side band without carrier
- Realize the modulation of a signal using a double side band without carrier. Note that transmitted signal can be expressed as
- Observe the signal in both time and frequency domain.
- Give the architecture of a coherent detector used to recover the message from .
- Implement this detector to demodulate the signal and verify the good operation. You can use 2 different flowgraphs (1 for the transmission and 1 for the reception) using a
File SinkandFile Sourcerespectively.
Double side band with carrier
- Realize the modulation of a signal using a double side band with carrier. Note that transmitted signal can be expressed as
- Observe the signal in both time and frequency domain.
- Modify the modulation index using a slider and observe the modification of the signal.
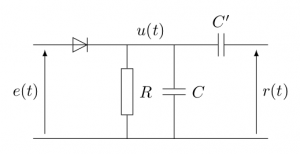
- AM signals are usually demodulted using a simple envelope detector. The architecture of this decoder is presented in Fig. 3.
- Implement this detector to demodulate the signal and verify the good operation.
- Check also if the AM signal can be decoded using the coherent detector.
- Finally, download the file
am_usrp710.dat. This file contains the complex envelope (I and Q channels) received by a USRP around the frequency 710 kHz with a sampling frequency of 256 kHz. Visualize the data with a blockFFT Sink(insert a blockThrottleto avoid overloading the processor). On the graph, we can see two stations transmit at 710 kHz (center) and 790 kHz (to the right). Knowing that the bandwidth of an AM signal is 10 kHz, insert a low pass filter allowing to select the station located around 710 kHz. Check that the filter is working properly on the graph. Insert the envelope detector at the output of the filter and a blockRational Resamplerto adapt the bit rate to the sound card (48 kHz) using anAudio Sink.
- Check the correct operation on the PC speakers (add if needed a
Multiply Const.block to set the volume of the station).
- Bonus: Demodulate the station at 790 kHz.
Frequency Modulation
Expression of a frequency modulated signal is given by:
Spectrum for general signal is usually unknown unless for very simple cases.
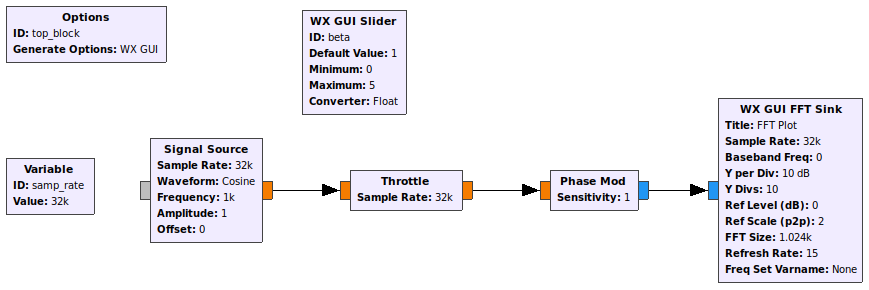
- Create the following flowgraph to generate a frequency (or phase) modulated signal.
- Observe the transmitted spectrum.
- Find the values of the modulation index to cancel the power at , , ...
- Create a decoder for the transmitted signal. Check the correct operation for different messages