MA331 Information Theory and Channel Coding

The objective of this course is to understand how we can transmit a message in-between a transmitter and a receiver spatially (or temporally) separated. Especially, how we can use coding to realize an error free transmission over noisy channels. This beautiful result has been predicted by C. E. Shannon and relies on two distinct operations which are source coding and channel coding. This course is an introduction to information theory and describe the main algorithms in both source coding and channel coding. This course is related to SC311 Wireless Communications but tackle the communication problem mainly at the bit level.

This course is composed of 3 parts. Slides (in french) for each part can be downloaded here:

1. Introduction
2. Information Theory
3. Source Coding
4. Channel Coding

The following of this page corresponds to the labs.

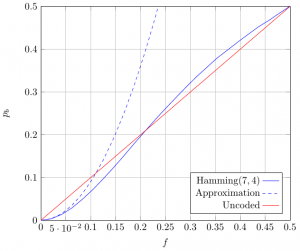
This objective of this lab is to allow you to evaluate the performance of classical telecommunication system by simulating the transmission of a large quantity of random data (Monte Carlo method). A special focus is placed on the performance of forward error correcting codes over different channels. The original subject of this lab is based on Matlab (or Octave) and is available here (in French) where the objective is to estimate the performance of the classical Hamming code $H(7,4)$ over the BSC channel of probability $f$.

This wiki presents a different approach based on the IT++ library which allows to generalize the results for any forward error correcting code and any channel.

IT++

IT++ is a C++ library designed to evaluate the performance of different telecommunications systems. Several forward error correction codes have been implemented and can easily be characterized and compared. All the results presented during the course have been obtained using this library.

Hamming Code

• After installing the library (which is maybe the hardest step of this lab), create a file main.cpp and copy the following program.

#include <itpp/itcomm.h>

using namespace itpp;
using std::cout;
using std::endl;

int main()
{
  bvec bits, ebits, dbits;

  Hamming_Code hc(3);

  RNG_randomize();

  bits = randb(4);              // Generate 4 random bits

  ebits = hc.encode(bits);      // Encode with H(7,4)

  dbits = hc.decode(ebits);     // Decode with H(7,4)

  cout << "bits = " << bits << endl;
  cout << "ebits = " << ebits << endl;
  cout << "dbits = " << dbits << endl;

  return 0;
}

The program can be built with the following command:

$ g++ `pkg-config --cflags itpp` -o main main.cpp `pkg-config --libs itpp`

If sucessfull, this command produces the binary file main which can be directly executed by typing:

$ ./main

• Determine the generator matrix $G$ of the Hamming code $H(7,4)$.

• Modify the encoded vector by adding 1 error on the codeword and observe the decoded codeword.

• Same question with 2 errors.

Performance over BSC channel

#include <itpp/itcomm.h>

#define N 500000

using namespace itpp;
using std::cout;
using std::endl;

int main()
{
  bvec bits, ebits, rbits, dbits;
  vec f = linspace(0.0, 0.5, 20);
  vec ber(p.length());

  BSC bsc;
  BERC berc;
  Hamming_Code hc(3);
  it_file ff;

  RNG_randomize();

  for (int i = 0; i < p.length(); i++)
  {
    bsc.set_prob(f(i));         // Set the error prob of the BSC
    bits = randb(N);            // Generate N random bits
    ebits = hc.encode(bits);    // Encode with H(7,4)
    rbits = bsc(ebits);         // Transmit over BSC
    dbits = hc.decode(rbits);   // Decode with H(7,4)
    berc.clear();               // Reset the counter
    berc.count(bits, dbits);    // Count the errors
    ber(i) = berc.get_errorrate();
  }
  cout << "BER = " << ber << endl;
  ff.open("res.it");            // Save the results
  ff << Name("f") << f;
  ff << Name("ber") << ber;
  ff.close();

  return 0;
}

Execution takes few seconds and display the BER for the different probabilities $f$ of the BSC channel. Results are also saved in the file res.it and can be easily displayed using the itload.m script using Matlab (or Octave):

> itload('res.it');
> plot(f, ber);

Performance in term of BER $p_{b}$ of the Hamming code H(7,4) over BSC of probability $f$.

Simulated results can also be compared with the theory. Word error probability can be computed by remarking that a received codeword cannot be decoded if it contains 2 or more errors:

${\begin{aligned}p_{B}&=\sum _{i=2}^{7}{\binom {7}{i}}f^{i}(1-f)^{7-i}\\&\approx {\binom {7}{2}}f^{2}\\&\approx 21f^{2}\\\end{aligned}}$

Bit error rate can be estimated by noting that when a received codeword contains 2 error, the decoding algorithm will add 1 additional error:

$p_{b}\approx {\frac {3}{7}}p_{B}\approx 9f^{2}$

IT++ library supports dozens of different codes, modulations and channels and allows to easily change the simulated system to quickly estimate the achievable performance.